| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 아셈듀오 후기
- 제네바주거
- 패스트캠퍼스 #자료구조 #코딩테스트 #배열
- 파이썬
- 제네바
- 데이터 포트폴리오
- 두잇알고리즘코딩테스트
- 키워드시각화
- 리뷰분석
- 데이터 분석 포트폴리오
- 아셈듀오
- 테이블계산
- 텍스트분석 시각화
- 제네바경영대학교
- 태블로 포트폴리오
- 아셈듀오 선정
- HEG
- 교환학생
- 공모전후기
- 교환학생 장학금
- CRM
- 데이터 시각화 포트폴리오
- tableau
- 태블로
- MairaDB
- 데이터공모전
- 무신사 데이터분석
- 제네바기숙사
- 미래에셋 공모전
- 교환학생주거
- Today
- Total
민듀키티
한 번에 끝내는 딥러닝/인공지능 (Sigmoid and Softmax) 본문
1. Odds (오즈)
오즈는 확률을 표현하는 또 다른 방법으로 p / (1 - p) 로 정의할 수 있다.
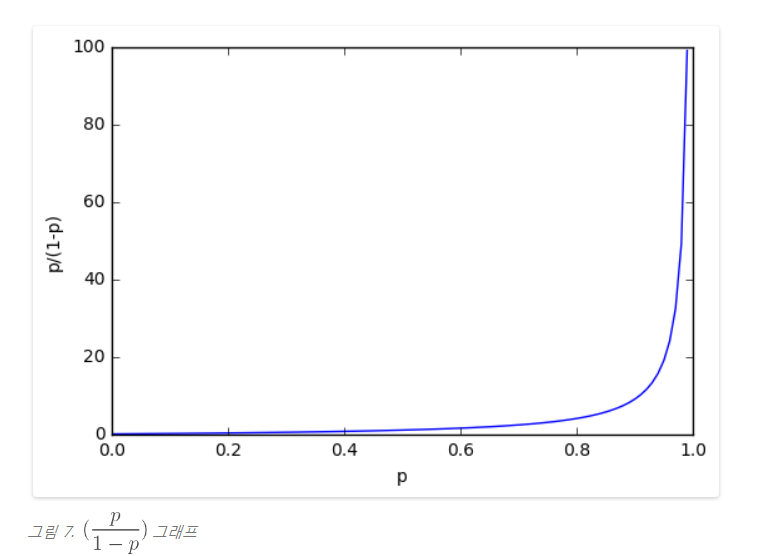
예를 들어 망치로 꼬부러진 동전이 있다고 할 때, 앞면이 나올 확률이 0.3, 뒷면이 나올 확률이 0.7 이라고 가정하면,
오즈 > 0 : 앞면이 나올 확률 > 뒷면이 나올 확률
오즈 < 0 : 뒷면이 나올 확률 > 앞면이 나올 확률
이렇듯, 그냥 확률을 표현하는 또 다른 방법이다.
2. Logit
로짓은 앞선 오즈에 log를 취한 식으로 대칭적인 구조를 가진다.
log ( p / (1 - p) )
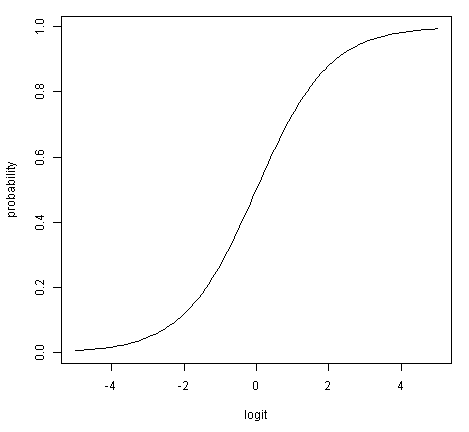
Logit의 대표적인 특징 2가지
1) 확률의 범위는 [0,1] 이나, 로짓의 범위는
3. Logit and Sigmoid
로짓과 시그모이드의 관계는 다음과 같이 도출할 수 있다.

즉, logit 을 넣었을 때 sigmoid와 같다.

왼쪽은 확률(오즈)를 받아 logit으로 바꿔주는 것을 시각화 한 것이고,
오른쪽은 logit을 받아 확률(오즈)로 바꿔주는 것을 시각화 한 것이다.
즉, 확률을 내보내주는 함수로 사용할 수 있다!
4. From Logit to Probability
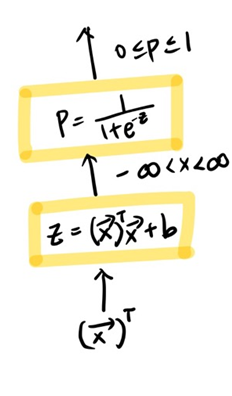
x 값이 들어오면 우선 Affine Function 을 통해 무한대 범위의 값의 output을 도출하고,
logit 함수를 이용해 확률로 output을 내보낸다. (즉, 동전의 앞면, 뒷면의 확률을 내보내는 것으로 구현할 수도 있어)
이 방식은 로지스틱 리그레션에서도 그대로 사용된다고 한다.
5. Softmax Layer
Softmax을 설명하기 전, 딥러닝 네트워크가 어떻게 작동되는지 시각화 해보자면,
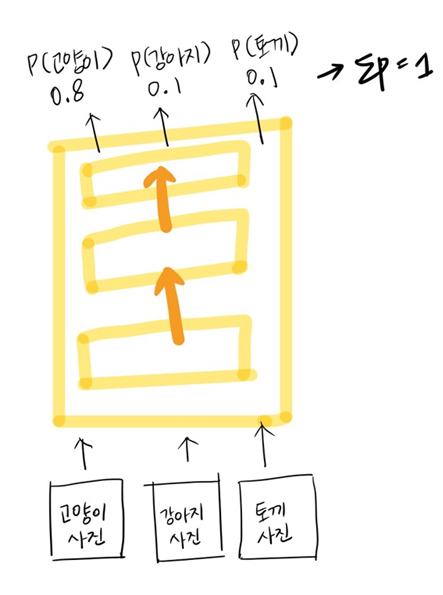
마지막에 고양이일 확률, 강아지일 확률, 토끼일 확률을 도출하게 되고, 이 확률 중 가장 큰 값을 정답으로 예측하게 되는 것이다. 이렇게 마지막에 클래스에 대한 확률을 뽑아내기 위해서 Softmax Layer 가 등장하게 되었다.

Input은 k개의 logit 값이다. 다시 이 logit 값에 e를 취해준 값을 softmax의 Input으로 넣어준다.
모든 e를 취해준 logit 값 더해서 이를 분모로, 각 e를 취해준 logit 값은 분자로하여 확률을 output으로 내보낸다.
그래서 결국 probbablity vector가 도출이 되게 된다.
또 중요한 사실은 probibility vector를 모두 더해주면 1이 나오게 된다.
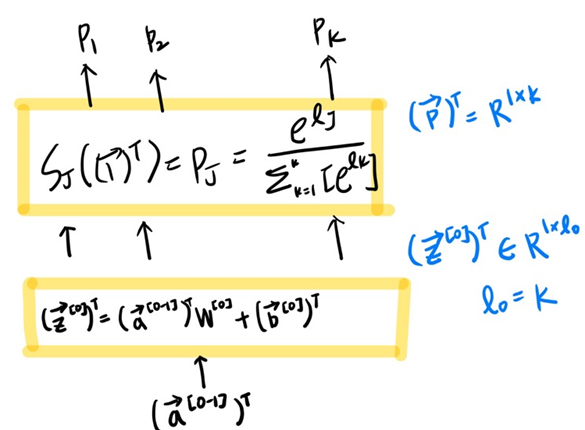
6. From Feature to Prediction
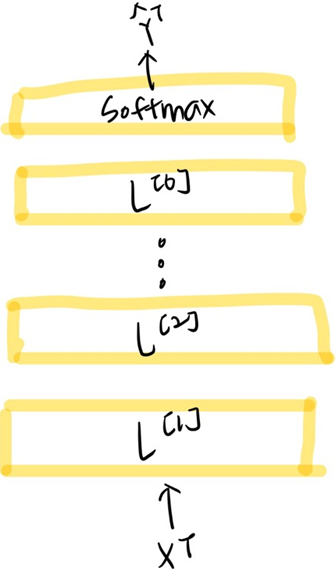
여러개의 layer를 통과하고 마지막에는 Softmax를 씌워져 output으로 도출하게 된다.
'Data Science > 한번에 끝내는 딥러닝&인공지능' 카테고리의 다른 글
| 한 번에 끝내는 딥러닝/인공지능 (Pooling Layers) (0) | 2022.02.08 |
|---|---|
| 한 번에 끝내는 딥러닝/인공지능 (Conv Layers) (0) | 2022.02.08 |
| 한 번에 끝내는 딥러닝/인공지능 (Loss Functions) (0) | 2022.02.08 |
| 한 번에 끝내는 딥러닝/인공지능 (Dense Layers) (1) | 2022.02.05 |
| 한 번에 끝내는 딥러닝/인공지능 (Affine_Functions) (0) | 2022.02.05 |
