| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 리뷰분석
- 태블로 포트폴리오
- 텍스트분석 시각화
- tableau
- 아셈듀오
- 무신사 데이터분석
- 아셈듀오 선정
- 교환학생
- 데이터 포트폴리오
- 파이썬
- 키워드시각화
- 교환학생 장학금
- 데이터 시각화 포트폴리오
- 제네바주거
- 미래에셋 공모전
- MairaDB
- 제네바
- 아셈듀오 후기
- 데이터공모전
- CRM
- 두잇알고리즘코딩테스트
- 제네바기숙사
- 데이터 분석 포트폴리오
- 태블로
- 테이블계산
- 교환학생주거
- 패스트캠퍼스 #자료구조 #코딩테스트 #배열
- 제네바경영대학교
- 공모전후기
- HEG
- Today
- Total
민듀키티
알고리즘 코딩테스트 - 자료구조 (투포인터, 슬라이딩 윈도우) 본문
1. 투 포인터
(1) 투포인터 핵심이론 (아래에 백준 문제 읽고오기)

- start_index를 오른쪽으로 한 칸 이동 = 왼쪽 인덱스 삭제
- end_index를 오른쪽으로 한 칸 이동 = 자연수의 범위를 한 칸 확장
- start_index = end_index : 경우의 수를 1을 증가시킴
(2) 투 포인터의 이동원칙
- sum > N (입력받은 값) : sum = sum - start_index ; start_index; (sum 값을 줄여야 함으로, 인덱스 삭제와 같은 효과를 지니는 start_index를 한 칸 이동해줌)
- sum < N (입력받은 값): sum = sum + end_index ; end_index ; (sum 값을 늘려야 함으로, 자연수의 범위를 확장시키는 효과를 지니는 end_index를 한 칸 이동해줌)
- sum == N : end_index ++; sum + end_index; count++; (sum값과 입력값이 같기 때문에, count 값을 +1 해줌)
아래 문제에서 자세히 투포인터를 이해해봅시다 !
백준 2018 : 연속된 자연수의 합 구하기
https://www.acmicpc.net/problem/2018
2018번: 수들의 합 5
어떠한 자연수 N은, 몇 개의 연속된 자연수의 합으로 나타낼 수 있다. 당신은 어떤 자연수 N(1 ≤ N ≤ 10,000,000)에 대해서, 이 N을 몇 개의 연속된 자연수의 합으로 나타내는 가지수를 알고 싶어한
www.acmicpc.net
- 시간복잡도 고려 : N의 최댓값이 10,000,000으로 매우 크게 잡혀있기 때문에 O(nlogn)의 시간 복잡도 알고리즘을 사용하면 제한 시간을 초과함. 따라서 O(n) 알고리즘을 사용해야 함 -> 투 포인터 알고리즘 사용
- 투 포인터 알고리즘 : 시작 인덱스, 종료 인덱스를 투 포인터로 지정
- 저는 이 개념이 조금 어려웠는데요, 시각화로 이 문제의 알고리즘을 생각해봅시다 !!
[초기화]

초기화 변수는 sum과 count 입니다. 여기서 주의해야 할 것은 count = 1 로 초기화 해주는 것입니다. 왜냐하면 N이 15일 때, 숫자 15만 뽑는 경우의 수를 미리 넣기 위해서 입니다.
[sum = N] -> end_index ++; sum + end_index; count++;

sum = 15 인 경우입니다. (출력 예제가 15임) count 및 end_index의 값을 1씩 증가시켜 줍니다.
[sum > N] -> sum = sum - start_index ; start_index;

end_index 값을 1 증가시켜준다면, 위와 같은 상황이 발생하게 됩니다. 즉, sum 값이 21로 N값보다 큰 경우가 발생합니다. 이러한 경우에는 start_index값을 증가시켜서 왼쪽 인덱스를 삭제해주는 효과를 만들어 줍니다.
[sum < N ] -> sum = sum + end_index ; end_index;

start_index를 한 칸 증가시켜주면 start_index값은 2를 가지게 됩니다. 그래도 여전히 sum 값은 20으로 N보다 큽니다. 따라서, 다시 한번 start_index 값을 증가시켜 줍니다.
- 위의 상황에 맞게 조건문을 사용해서 코드를 짜줌
n = int(input())
count = 1
start_index = 1
end_index = 1
sum = 1
while end_index != n :
if sum == n :
count += 1
end_index += 1
sum += end_index
elif sum > n :
sum -= start_index
start_index +=1
else :
end_index += 1
sum += end_index
print(count)
백준 1940 : 주몽의 명령
https://www.acmicpc.net/problem/1940
1940번: 주몽
첫째 줄에는 재료의 개수 N(1 ≤ N ≤ 15,000)이 주어진다. 그리고 두 번째 줄에는 갑옷을 만드는데 필요한 수 M(1 ≤ M ≤ 10,000,000) 주어진다. 그리고 마지막으로 셋째 줄에는 N개의 재료들이 가진 고
www.acmicpc.net
- 이 문제도 역시나 투 포인터를 사용
- 이 문제에서의 힌트는 투 포인터 + 정렬 (투포인터를 사용하기 위해서)
- 시각화로 문제 풀기하기

- 위의 문제는 start_index와 end_index가 같은 곳에서 시작했지만, 이번에는 각각 반대에서 시작함
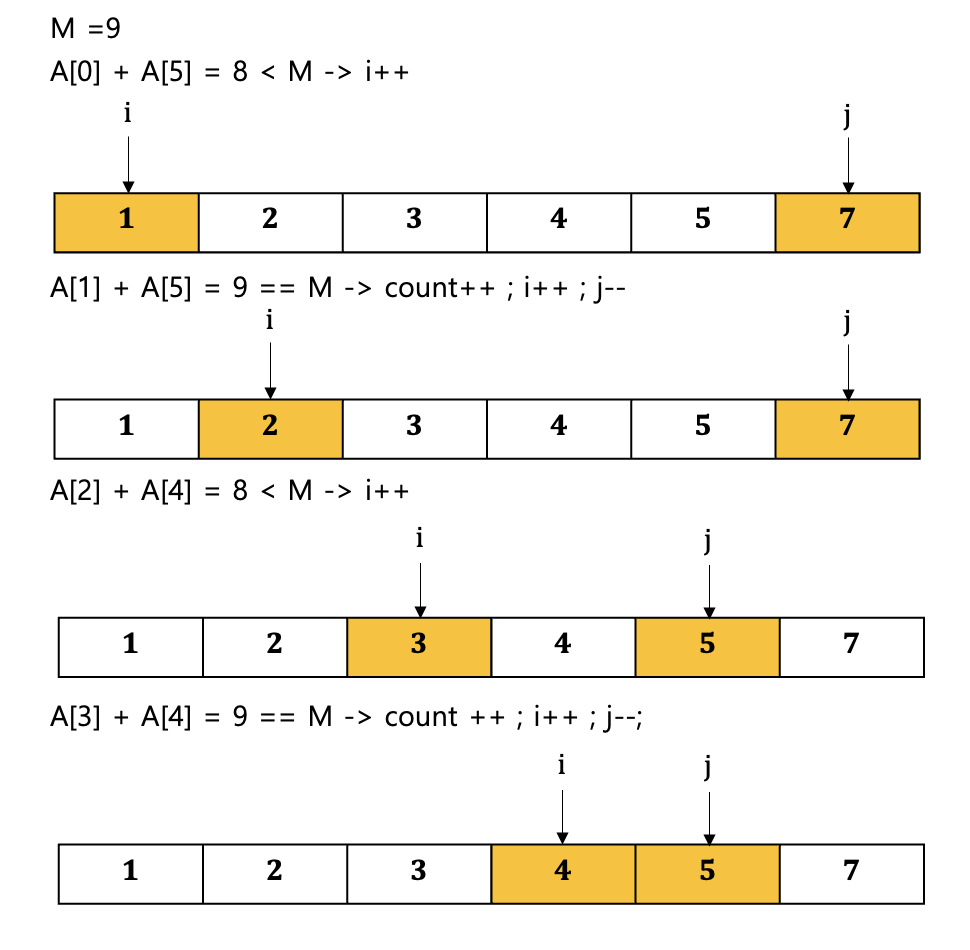
따라서, 이러한 경우의 투포인터 이동원칙을 정리해보면
- A[i] + A[j] == M : count ++ ; i++ ; j--
- A[i] + A[j] < M : i++;
- A[i] + A[j] > M : j--;
- 위의 상황에 맞게 조건문을 사용해서 코드를 짜줌 (이렇게 이동원칙 정리해놓으면, 코드 짜는 것은 쉬움)
input_list = list(map(int, input().split()))
input_list.sort()
count = 0
start_index = 0
end_index = n-1
while start_index < end_index :
if input_list[start_index] + input_list[end_index] > m :
end_index -=1
elif input_list[start_index] + input_list[end_index] < m :
start_index +=1
else :
count +=1
start_index +=1
end_index -1
print(count)
print(input_list)
2. 슬라이딩 윈도우
(1) 슬라이딩 윈도우 핵심이론
- 2개의 포인터로 범위를 지정한 후, 범위를 유지한 채로 이동하는 것임. 즉 투포인터 개념에 범위 지정이 더해짐
- 따라서, 투 포인터 알고리즘이랑 매우 유사함
시각화로 슬라이딩 윈도우 이해하기

백준 12891번 : DNA 비밀번호
https://www.acmicpc.net/problem/12891
12891번: DNA 비밀번호
평소에 문자열을 가지고 노는 것을 좋아하는 민호는 DNA 문자열을 알게 되었다. DNA 문자열은 모든 문자열에 등장하는 문자가 {‘A’, ‘C’, ‘G’, ‘T’} 인 문자열을 말한다. 예를 들어 “ACKA”
www.acmicpc.net
- 이 문제는 이해가 어렵지는 않지만, 문제가 깁니다. 그래서 시각화로 쉽게 문제를 이해해보겠습니다.

한 칸을 오른쪽으로 옮겨봅니다.

- 따라서, 첫번째 예제 출력 값이 0이 나오게 됩니다.
근데 코드 짜기가 어렵네요 ㅠㅠㅠ 실버 주제에 코드가 기네요,,,
내일 학교에서 코드를 짜고,,, 수정하겠습니다.
* do it 알고리즘 코딩테스트 내용을 참고하였습니다.
'Coding Test' 카테고리의 다른 글
| 알고리즘 코딩테스트 - 정렬(버블, 선택, 삽입) (0) | 2023.03.10 |
|---|---|
| 알고리즘 코딩테스트 - 자료구조(스택과 큐) (0) | 2023.03.10 |
| 알고리즘 코딩테스트 - 자료구조 (배열, 리스트, 구간합) (1) | 2023.03.03 |
| 알고리즘 코딩테스트 - 코딩테스트 기본 (0) | 2023.03.03 |
| 알고리즘 / 기술면접 스터디 공부 - 알고리즘 이론(재귀용법) (0) | 2022.10.02 |
