| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 파이썬
- 교환학생주거
- 공모전후기
- 제네바주거
- 텍스트분석 시각화
- 데이터공모전
- 아셈듀오
- 태블로 포트폴리오
- 태블로
- 데이터 분석 포트폴리오
- CRM
- 제네바기숙사
- 교환학생 장학금
- 두잇알고리즘코딩테스트
- 무신사 데이터분석
- tableau
- 미래에셋 공모전
- 테이블계산
- 데이터 포트폴리오
- 제네바
- 제네바경영대학교
- MairaDB
- 패스트캠퍼스 #자료구조 #코딩테스트 #배열
- 리뷰분석
- 아셈듀오 후기
- 데이터 시각화 포트폴리오
- 교환학생
- HEG
- 아셈듀오 선정
- 키워드시각화
- Today
- Total
민듀키티
핸즈온 머신러닝 (Chapter 4. 모델훈련) 본문
1. 선형회귀
간단한 선형회귀 모델의 예시

▶ θ : 모델의 파라미터
▶ 가중치의 합과 편향이라는 상수를 더해 예측을 만듬
이를 벡터형태로 표기한다면 ?
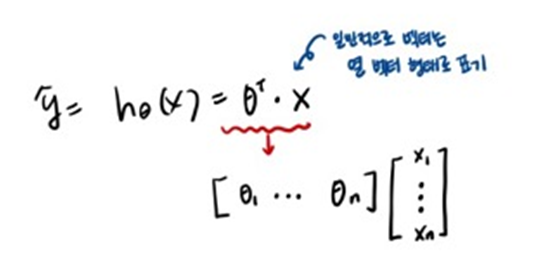
▶ θ와 x의 점곱으로 표현할 수 있으며, 벡터는 주로 열 벡터로 표기하기 때문에 θ를 전치시켜서 선형회귀 식을 표현
그러면, 최적의 θ을 찾는 방법은 ?
▶ RMSE를 최소화하는 θ를 찾아야 함

(1) 정규방정식
비용함수를 최소화하는 θ를 찾기 위한 해석적인 방법으로, 이를 정규방정식이라고 함

정규방정식 공식을 테스트하기 위한 코드
1) 데이터 생성하기
import numpy as np
# 0에서 2까지의 크기의 행렬을 생성함
X = 2 * np.random.rand(100, 1)
# noise 까지 더해주기위해 np.random.randn을 해줌
y = 4 + 3 * X + np.random.randn(100, 1)
2) 정규방정식을 사용해 θ 계산하기
# 1이 채워진 100*1 행렬을 생성함
X_b = np.c_[np.ones((100, 1)), X]
# 정규방정식
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
3) 정규방정식을 통해 도출된 θ값 확인하기
theta_best
>>> array([[4.21509616],
[2.77011339]])
사이킷런에서 선형회귀를 수행하기 위한 코드
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
# 편향
lin_reg.intercept_
# 기울기
lin_reg.coef_
2. 경사하강법
경사하강법 : 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘
비용 함수를 최소화하기 위해 반복해서 파라미터를 조정해나가는 것
그레디언트가 감소하는 방향으로 진행하고, 그레이디언트가 0이되면 최솟값에 도달

▶ 임의로 한 점을 정하고, 최솟값을 위해 조금씩 이동하는 방법으로 기울기가 낮은 방향으로 한발 한발 이동하는 방법
▶ 학습률 : 경사하강법에서 중요한 파라미터는 스텝의 크기
경사하강법의 대표적인 문제점 2가지
(1) 학습률 값 설정에 대한 어려움
- 학습률이 너무 작을 때 : 알고리즘이 수렴하기 위해 반복을 많이 진행해야 하므로 시간이 오래 걸림
- 학습률이 너무 클 때 : 더 큰 값으로 발산하게 만들어 적절한 해법을 찾지 못하게 함
(2) 전역최솟값보다 덜 좋은 지역 최솟값에 도달할 수도 있음

경사하강법 사용할시 : 같은 스케일을 적용해야 함

- 왼쪽 : 최솟값으로 곧장 진행하고 있어 빠르게 도달함
- 오른쪽 : θ2가 더 가파르게 가게되고, 돌아서가게 됨
(1) 배치경사하강법
- 파라미터를 업데이트할 때마다 모든 학습 데이터를 사용하여 cost function의 gradient을 계산함
- 메모리가 한정적이기 때문에 거의 사용하지 않는 방법이라고 함
[ 비용함수의 편도함수 ]


매 경사하강법 스템에서 전체 훈련세트 X에 대해 계산하는 방법
[스텝의 크기 결정]

gradient에 eta를 곱해서 스텝의크기를 결정함
알고리즘을 코드로 구현해보면,
eta = 0.1 # 학습률
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # 랜덤 초기화
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
(2) 확률적 경사하강법
- 배치경사하강법과는 다르게 일부 데이터만 사용하는 방법
- 확률적(= 무작위) 경사하강법이기 때문에 배치 경사하강법보다 훨씬 불안정함
- 비용 함수가 최솟값에 도달할 때까지 위아래로 요동치면서 평균적으로 감소하기 때문에, 배치 경사 하강법보다 훨씬 불안정하다.
(3) 미니배치 경사하강법
- 미니배치라고 부르는 임의의 작은 샘플 세트에 대해 그레디언트를 계산함
[파라미터 공간에 표시된 경사하강법의 경로]

- 배치 경사하강법 : 경로가 실제로 최솟값에서 멈춤
- 확률적 경사하강법 & 미니배치 경사하강법 : 근처에서 맴돌고 있음
3. 다항회귀
- 각 특성의 거듭제곱을 새로운 특성으로 추가하고, 이 확장된 특성을 포함한 데이터셋에 선형모델을 훈련시키는 방법
(1) 2차 방정식 생성
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1) #노이즈까지 더해주기
(2) PolynomialFeatures를 사용해 훈련 데이터를 변환
from sklearn.preprocessing import PolynomialFeatures
# degree : 차수 설정
# include_bias : 편향을 위한 가상특성
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
(3) 훈련 데이터에 Linear Regression을 적용
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
>>> (array([1.78134581]), array([[0.93366893, 0.56456263]]))
4. 학습곡선
- 고차 다항 회귀를 적용하면 훈련 데이터에 과적합될 수 있음

과대적합 : 훈련데이터에서 성능이 좋지만, 교차 점수가 나쁜 경우
과소적합 : 훈련데이터에서도 성능이 안좋고, 교차점수도 안좋은 경우
[학습곡선을 통해 적합한 모델 유무 판단 가능]

(1) 오른쪽 과소적합 : 두 곡선이 수평한 구간을 만들고 꽤 높은 오차에서 매우 가까이 근접해있음
(2) 왼쪽 과대적합 : 두 곡선 사이에 공간이 존재하는데, 훈련 데이터에서의 모델 성능이 검증 데이터에서보다 훨씬 낫다는 것을 의미
5. 규제가 있는 선형모델
과대적합을 감소하기 위해, 가중치를 제한함으로써 규제를 가함
(1) 릿지회귀

- 가중치 벡터의 제곱합을 비용함수로 더해줘 규제를 시켜줌
- 여기서 a는 모델을 얼마나 많이 규제할지를 조절하는 파라미터
- a는 하이퍼파라미터
(2) 라쏘회귀

- 덜 중요한 특성의 가중치를 제거하려고하여, 변수 선택 효과의 특징을 가지고 있음
6. 로지스틱 회귀
- 샘플이 특정 클래스에 속할 확률을 추정하는데 사용됨
- 추정 확률이 50%가 넘으면 양성 클래스, 넘지 못하는 음성 클래스 등과 같이 분류
(1) 확률추정

- 선형회귀처럼 바로 결과를 출력하지 않고, 결괏값의 "로지스틱"을 출력함
- 로지스틱은 시그모이드 함수로, 0과 1사이의 값을 출력하는 함수임
[로지스틱 함수]

0.5보다 작으면, 0으로 분류하고 0.5보다 크면 1로 분류하는 등의 예측을 실행함
(2) 훈련과 비용함수

y = 1에 대해서는 높은 확률을 추정하고, y = 0에 대해서는 낮은 확률을 추정하는 방법으로 하기 위해서
로그함수의 특징을 이용하여 비용함수를 정의해줌
위의 식을 하나의 식으로 합쳐보면,

위와 같이 정의할 수 있음
(3) 결정경계
꽃잎의 너비를 기반으로 iris - Versicolor종을 감지하는 분류기 생성
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y)
결정경계를 확인해보면, 위와 같음.
결정경계를 기반으로, iris virginica 판단 유무를 분리할 수 있음
(4) 소프트맥스 회귀
- 여러 개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 하는 법
'Data Science > 핸즈온 머신러닝' 카테고리의 다른 글
| 핸즈온 머신러닝 (Chapter 6. 결정트리) (0) | 2022.04.06 |
|---|---|
| 핸즈온 머신러닝 (Chapter 5. 서포트 벡터 머신) (0) | 2022.04.06 |
| 핸즈온 머신러닝 (Chapter 3. 분류) (0) | 2022.03.20 |
